THE ELECTRO-SEISMIC SURVEY METHOD
 |
Introduction
The Electroseismic method, sometimes called the Electrokinetic Survey (EKS) method, is a geophysical technique that attempts to provide the depth to groundwater and an estimate of the permeability, and hence yield, that might be expected from a well drilled into the aquifer. The Physics of the method has been understood since the 1930's when Thompson (1936) and Ivanov (1939 and 1950) were the fi rst to realize that a seismic compression wave (p-wave) impulse will provide sufficient oscillating pressure in rock pore fluids to produce a measurable oscillating electrical potential at the ground surface.
The Electroseismic method is related to the commonly known phenomenon called streaming potential, where flowing subsurface water produces a voltage measurable on the ground surface. A more distant relative of the method are thunderstorms where rapidly rising air produces electrical charge separations, thus creating large potential differences.
Since the papers by Thompson and Ivanov were written, many investigations into the method have been completed and many papers have been published; the more significant of these are listed at the end of this document.
Until recently, the electrical signal from a seismic pulse impinging on subsurface groundwater was difficult to measure since electrical noise, especially powerline noise, contaminated the data. However, Groundflow Ltd, based in the UK, discovered a new detection method that is now patented both in the UK and USA. This method uses electrically isolated lines from each electrode pair, referencing their potentials to a floating virtual earth, and positioning the electrode pairs close to the seismic source, thereby achieving a significant improvement in the signal to noise ratio.
A significant amount of research is now being done into this method with organizations such as the Massachusetts Institute of Technology (MIT), Exxon Production and Research Company and the Australian Nuclear Science and Technology Organization becoming involved.
Basic Theory of the Method

The circular area (in plan view) encompassed by the leading edge of the pulse when the negative part the pulse just intersects the interface is called the first Fresnel zone. As can be seen in Figure 2, the curvature of the wavefront and the Fresnel geometry ensures that the signal is focused back to the shot point.

Figure 2. Schematic showing the focusing of the electrical signals back to the shot point.
The Electroseismic method, sometimes called the Electrokinetic Survey (EKS) method, is a geophysical technique that attempts to provide the depth to groundwater and an estimate of the permeability, and hence yield, that might be expected from a well drilled into the aquifer. The Physics of the method has been understood since the 1930's when Thompson (1936) and Ivanov (1939 and 1950) were the fi rst to realize that a seismic compression wave (p-wave) impulse will provide sufficient oscillating pressure in rock pore fluids to produce a measurable oscillating electrical potential at the ground surface.
The Electroseismic method is related to the commonly known phenomenon called streaming potential, where flowing subsurface water produces a voltage measurable on the ground surface. A more distant relative of the method are thunderstorms where rapidly rising air produces electrical charge separations, thus creating large potential differences.
Since the papers by Thompson and Ivanov were written, many investigations into the method have been completed and many papers have been published; the more significant of these are listed at the end of this document.
Until recently, the electrical signal from a seismic pulse impinging on subsurface groundwater was difficult to measure since electrical noise, especially powerline noise, contaminated the data. However, Groundflow Ltd, based in the UK, discovered a new detection method that is now patented both in the UK and USA. This method uses electrically isolated lines from each electrode pair, referencing their potentials to a floating virtual earth, and positioning the electrode pairs close to the seismic source, thereby achieving a significant improvement in the signal to noise ratio.
A significant amount of research is now being done into this method with organizations such as the Massachusetts Institute of Technology (MIT), Exxon Production and Research Company and the Australian Nuclear Science and Technology Organization becoming involved.
Basic Theory of the Method
Electroseismic effects are initiated by seismic waves, usually p-waves, passing through a porous rock and inducing relative motion between the rock matrix and the fluid within the rock pores. Motion of ionic fluid through capillaries in the rock occurs with cations preferentially adhering to the capillary walls, so that the applied pressure and resulting fluid flow relative to the rock matrix separates the cations and anions thus producing an electric dipole. This is called the Electroseismic effect.
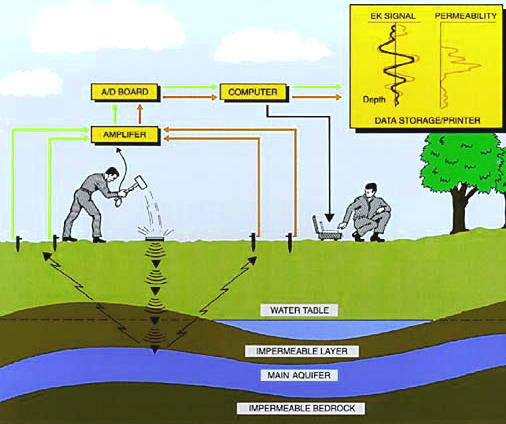
This is illustrated in Figure 1. A seismic source produces a seismic compression wave, which then propagates into the ground at a speed depending on the rocks through which it passes. Generally this speed varies from about 5000 ftIsec to over 10,000 ftIsec in sedimentary rocks, but can be faster in igneous and metamorphic rocks. The wave spreads out to form a hemisphere as illustrated in Figure 1. When the initial pressure pulse reaches the water table, or a rock saturated with water, electrical charges are separated as described above, and the electrical signal is transmitted back to the ground surface at approximately the speed of light. Conversely, when the wavefront emerges from the saturated zone (aquifer) at depth into a layer with little water, the signal decays to zero. The signal also usually decays to zero if the water in the aquifer becomes saline. Generally, the amplitude of the signal will also decay slowly with depth, as the spreading seismic wave loses its high frequency components and its amplitude decreases due to spherical divergence along with other factors. The fundamental relationships between the spreading seismic wave, the resulting electrical dipoles (charge separations) and the voltage at the ground surface are complex.
This is illustrated in Figure 1. A seismic source produces a seismic compression wave, which then propagates into the ground at a speed depending on the rocks through which it passes. Generally this speed varies from about 5000 ftIsec to over 10,000 ftIsec in sedimentary rocks, but can be faster in igneous and metamorphic rocks. The wave spreads out to form a hemisphere as illustrated in Figure 1. When the initial pressure pulse reaches the water table, or a rock saturated with water, electrical charges are separated as described above, and the electrical signal is transmitted back to the ground surface at approximately the speed of light. Conversely, when the wavefront emerges from the saturated zone (aquifer) at depth into a layer with little water, the signal decays to zero. The signal also usually decays to zero if the water in the aquifer becomes saline. Generally, the amplitude of the signal will also decay slowly with depth, as the spreading seismic wave loses its high frequency components and its amplitude decreases due to spherical divergence along with other factors. The fundamental relationships between the spreading seismic wave, the resulting electrical dipoles (charge separations) and the voltage at the ground surface are complex.

Figure 1. Schematic drawing illustrating the basic principles of the Electroseismic method at the top of an aquifer. This diagram should be rotated about its axis (seismic source) by 1800 to image the hemispherical nature of the seismic wave.
The circular area (in plan view) encompassed by the leading edge of the pulse when the negative part the pulse just intersects the interface is called the first Fresnel zone. As can be seen in Figure 2, the curvature of the wavefront and the Fresnel geometry ensures that the signal is focused back to the shot point.

Figure 2. Schematic showing the focusing of the electrical signals back to the shot point.
Measuring the Electroseismic Effect.
The geometry of the seismic source and electrode array used to measure the Electroseismic effect are illustrated in Figure 3. The electrodes in the array are spaced symmetrically about the seismic source at distances from the source of about 2.5 and 8 feet. The seismic wave is created and the instrument measures the resulting electrical signal.

Figure 3. The geometry of the seismic source and electrodes used to measure the Electroseismic effect.
One of the instruments used to measure the Electroseismic effect is called the Groundflow 2500J, or GF2500. This instrument incorporates the floating electrode system described earlier in this text.
Interpretation
Water can move within the pores of the rock easier in good aquifers (high permeability and porosity) than in poor ones and this provides the basis for assessing aquifer quality. If the water moves easily then it will move rapidly when under the influence of the seismic pulse. If the rock has a low permeability or hydraulic conductivity, then the water will move slowly. This causes the shape of the Electroseismic signal to be different in these two cases. A good aquifer will produce a more rapid rise in the signal amplitude than a poor one, all else being equal. A steeper rise time implies that the signal contains higher frequencies than a slow rising signal and the signal is said to have a greater bandwidth. Water yield estimates can be obtained from the signal bandwidth and the calculations to do this are programmed into the GF2500 instrument. The depth to the top of the aquifer is found from the time taken for the seismic signal to travel to the aquifer, which can be found from the time to the first arrival of the Electroseismic signal. Likewise, the depth to the bottom of the aquifer can be estimated from the time when the EKS signal decays to zero. In other words, the aquifer thickness can be found from the length of the Electroseismic signal. The velocity of seismic waves in different rock types is generally well known from seismic surveys, although there can be significant variations in the velocity of rocks, depending on several factors.
Limitations of the Method
The main limitations of the Electroseismic method relate to the depth of investigation and the depth resolution, the chemistry of the water, the geology of the aquifer and to the geometry of the signal generation array.
The depth of investigation depends on the strength of the seismic source and on the nature of the soil and subsoil. A soft soil and subsoil will attenuate the seismic signal and limit penetration depth. A hammer source can usually provide investigation depths to 250 to 300 feet. A buffalo source can investigate to depths of over 1500 feet.
Resolving the thickness of an aquifer depends on the length of the seismic pulse, which depends on the speed of seismic waves in the rocks. The higher the speed of the seismic pulse the longer is its wavelength and consequently, the lower is its resolution. In low speed rocks resolution may be 5 to 15 feet whereas in rocks with high velocities the resolution may be 15 to 45 feet, or even less .
. Predicting the depth to an aquifer depends on knowing the seismic velocity of the rocks under the sounding site. Since the velocity of even well defined rocks, for example sandstone, can vary widely from site to site, unless these velocities are measured, then an estimate has to be used. If a local well is available where a sounding can be
conducted, then this will provide a "calibration", and should make the interpreted depth more reliable.
The focusing effect of layered aquifers discussed earlier is advantageous when using the electrode array centered about the seismic source and works well for most layered, usually sedimentary, rocks. However, the method is not as effective in areas where the aquifer lies in cavities and large fractures although it can detect aquifers in fractured brittle rocks if they form layers. Limestone Karst terrain is an example of where the method is not usually successful.
Aquifers
An aquifer is a water saturated permeable geologic layer, or fracture zone, that is able transmit significant quantities of water. A geologic layer that cannot transmit significant quantities of water is usually referred to as an aquiclude. An aquitard is a rock unit that generally has a low permeability and hence will transmit only very limited quantities of water and are generally not suitable for production wells. The terms Aquifer or aquitards can be used to define most geologic strata. The most common aquifers include permeable sedimentary rocks such as sandstones, limestones, sand and gravel layers, and highly fractured volcanic and crystalline rocks. Common aquitards are unfractured shales, clays and dense (unfractured) crystalline rocks.
Sedimentary aquifers form layers and usually have a large lateral extent, whereas aquifers in fracture zones in igneous and crystalline rocks may have a very limited lateral extent. When searching for water using any geophysical method, including the Electroseismic method, the type of aquifer that may be present should be considered, both when planning a survey and especially when considering drilling.
The Electroseismic method responds to a subsurface circular area whose radius depends on the dimensions of the first Fresnel zone and for practical purposes is approximately equal to one third of the depth to the aquifer. If the survey is conducted in an area where the aquifers reside in fracture zones, it is possible that the Electroseismic signals will predict the occurrence of an aquifer, which occurs within a fractured area whose lateral extent is limited, but the drill hole may not intersect the fracture zone that provides the Electroseismic signal. Since the radius of the circle of influence for the Electroseismic method increases with the depth of the investigation, the difficulty of intersecting the fracture zone with a drill becomes greater as the depth to the aquifer increases.
References
The Massachusetts Institute of Technology (MIT) publications on this subject are listed on http://eaps.mit.edu/erl/research/papers.html. Of particular importance are papers by Stephen Pride, borehole experiments by Oleg Mikhailov and computer modeling by Matthew Haartsen.
The following lists some of the more significant references.
Beamish, D., Characteristics of near-surface Electroseismic coupling. 1999, Geophys. J. Int., 137,231-242
Biot, M. A, 1956, Theory of propagation of elastic waves in a fluid saturated porous solid, J and II: J. Acoust. Soc. AM., 28,168-191
Biot, M. A; 1962a, Mechanics of deformation and acoustic propagation in porous media: J. Appl. Phys., 33, 1482-1498
Biot, M. A, 1962b, Generalized theory of acoustic propagation in porous dissipative media: J. Acoust. Soc. Am., 34, 1254-1264
Butler, K. E., Russell, R. D., K~upic, A W., and Maxwell, M., 1994, Mapping of a stratigraphic boundary by its seismoelectric response, SAGEEP Annual Meeting, 1994 Proceedings, 689-699
Clarke, R. H., and Millar, J. W. A, 1995, Fluid Detection Method, patent Application PCT/GB95/00844, Filed 13/4/95, based on UK 9407649.4, filed 18/4/94.
Frenkel, J., 1944, On the theory of seismic and seismoelectric phenomenon in moist soil. J. Phys, 8, 230-241
Hankin, S., and Waring, Chris, 1999, EKS Geophysical Survey of Sites Near Kerang, Victoria, Australia. Australian Nuclear Science and Technology Organization, ANSTO/C601.
Ivanov, A G., 1939 Effect of electization of earth layers by elastic waves passing through them (in Russian): Doklady Akademii Nauk. SSSR, 24, 42-45
Ivanov, A G., 1950 Method for studying seismoelectric effects (In Russian): Izvestiya Akademii Nauk. SSSR ser. Geogr. I geofiz., 14,542-546
Martner, S. T. and Sparks, N. R., 1959, The Electroseismic effect: Geophysics, 24, 297308
The geometry of the seismic source and electrode array used to measure the Electroseismic effect are illustrated in Figure 3. The electrodes in the array are spaced symmetrically about the seismic source at distances from the source of about 2.5 and 8 feet. The seismic wave is created and the instrument measures the resulting electrical signal.

Figure 3. The geometry of the seismic source and electrodes used to measure the Electroseismic effect.
One of the instruments used to measure the Electroseismic effect is called the Groundflow 2500J, or GF2500. This instrument incorporates the floating electrode system described earlier in this text.
Interpretation
Water can move within the pores of the rock easier in good aquifers (high permeability and porosity) than in poor ones and this provides the basis for assessing aquifer quality. If the water moves easily then it will move rapidly when under the influence of the seismic pulse. If the rock has a low permeability or hydraulic conductivity, then the water will move slowly. This causes the shape of the Electroseismic signal to be different in these two cases. A good aquifer will produce a more rapid rise in the signal amplitude than a poor one, all else being equal. A steeper rise time implies that the signal contains higher frequencies than a slow rising signal and the signal is said to have a greater bandwidth. Water yield estimates can be obtained from the signal bandwidth and the calculations to do this are programmed into the GF2500 instrument. The depth to the top of the aquifer is found from the time taken for the seismic signal to travel to the aquifer, which can be found from the time to the first arrival of the Electroseismic signal. Likewise, the depth to the bottom of the aquifer can be estimated from the time when the EKS signal decays to zero. In other words, the aquifer thickness can be found from the length of the Electroseismic signal. The velocity of seismic waves in different rock types is generally well known from seismic surveys, although there can be significant variations in the velocity of rocks, depending on several factors.
Limitations of the Method
The main limitations of the Electroseismic method relate to the depth of investigation and the depth resolution, the chemistry of the water, the geology of the aquifer and to the geometry of the signal generation array.
The depth of investigation depends on the strength of the seismic source and on the nature of the soil and subsoil. A soft soil and subsoil will attenuate the seismic signal and limit penetration depth. A hammer source can usually provide investigation depths to 250 to 300 feet. A buffalo source can investigate to depths of over 1500 feet.
Resolving the thickness of an aquifer depends on the length of the seismic pulse, which depends on the speed of seismic waves in the rocks. The higher the speed of the seismic pulse the longer is its wavelength and consequently, the lower is its resolution. In low speed rocks resolution may be 5 to 15 feet whereas in rocks with high velocities the resolution may be 15 to 45 feet, or even less .
. Predicting the depth to an aquifer depends on knowing the seismic velocity of the rocks under the sounding site. Since the velocity of even well defined rocks, for example sandstone, can vary widely from site to site, unless these velocities are measured, then an estimate has to be used. If a local well is available where a sounding can be
conducted, then this will provide a "calibration", and should make the interpreted depth more reliable.
The focusing effect of layered aquifers discussed earlier is advantageous when using the electrode array centered about the seismic source and works well for most layered, usually sedimentary, rocks. However, the method is not as effective in areas where the aquifer lies in cavities and large fractures although it can detect aquifers in fractured brittle rocks if they form layers. Limestone Karst terrain is an example of where the method is not usually successful.
Aquifers
An aquifer is a water saturated permeable geologic layer, or fracture zone, that is able transmit significant quantities of water. A geologic layer that cannot transmit significant quantities of water is usually referred to as an aquiclude. An aquitard is a rock unit that generally has a low permeability and hence will transmit only very limited quantities of water and are generally not suitable for production wells. The terms Aquifer or aquitards can be used to define most geologic strata. The most common aquifers include permeable sedimentary rocks such as sandstones, limestones, sand and gravel layers, and highly fractured volcanic and crystalline rocks. Common aquitards are unfractured shales, clays and dense (unfractured) crystalline rocks.
Sedimentary aquifers form layers and usually have a large lateral extent, whereas aquifers in fracture zones in igneous and crystalline rocks may have a very limited lateral extent. When searching for water using any geophysical method, including the Electroseismic method, the type of aquifer that may be present should be considered, both when planning a survey and especially when considering drilling.
The Electroseismic method responds to a subsurface circular area whose radius depends on the dimensions of the first Fresnel zone and for practical purposes is approximately equal to one third of the depth to the aquifer. If the survey is conducted in an area where the aquifers reside in fracture zones, it is possible that the Electroseismic signals will predict the occurrence of an aquifer, which occurs within a fractured area whose lateral extent is limited, but the drill hole may not intersect the fracture zone that provides the Electroseismic signal. Since the radius of the circle of influence for the Electroseismic method increases with the depth of the investigation, the difficulty of intersecting the fracture zone with a drill becomes greater as the depth to the aquifer increases.
References
The Massachusetts Institute of Technology (MIT) publications on this subject are listed on http://eaps.mit.edu/erl/research/papers.html. Of particular importance are papers by Stephen Pride, borehole experiments by Oleg Mikhailov and computer modeling by Matthew Haartsen.
The following lists some of the more significant references.
Beamish, D., Characteristics of near-surface Electroseismic coupling. 1999, Geophys. J. Int., 137,231-242
Biot, M. A, 1956, Theory of propagation of elastic waves in a fluid saturated porous solid, J and II: J. Acoust. Soc. AM., 28,168-191
Biot, M. A; 1962a, Mechanics of deformation and acoustic propagation in porous media: J. Appl. Phys., 33, 1482-1498
Biot, M. A, 1962b, Generalized theory of acoustic propagation in porous dissipative media: J. Acoust. Soc. Am., 34, 1254-1264
Butler, K. E., Russell, R. D., K~upic, A W., and Maxwell, M., 1994, Mapping of a stratigraphic boundary by its seismoelectric response, SAGEEP Annual Meeting, 1994 Proceedings, 689-699
Clarke, R. H., and Millar, J. W. A, 1995, Fluid Detection Method, patent Application PCT/GB95/00844, Filed 13/4/95, based on UK 9407649.4, filed 18/4/94.
Frenkel, J., 1944, On the theory of seismic and seismoelectric phenomenon in moist soil. J. Phys, 8, 230-241
Hankin, S., and Waring, Chris, 1999, EKS Geophysical Survey of Sites Near Kerang, Victoria, Australia. Australian Nuclear Science and Technology Organization, ANSTO/C601.
Ivanov, A G., 1939 Effect of electization of earth layers by elastic waves passing through them (in Russian): Doklady Akademii Nauk. SSSR, 24, 42-45
Ivanov, A G., 1950 Method for studying seismoelectric effects (In Russian): Izvestiya Akademii Nauk. SSSR ser. Geogr. I geofiz., 14,542-546
Martner, S. T. and Sparks, N. R., 1959, The Electroseismic effect: Geophysics, 24, 297308